Basics of Generative Modeling#
In generative tasks, it is necessary to inject some form of stochasticity into the generation process. In this regard, two general approaches can be distinguished: Autoregressive generation of discrete sequences and Non-Autoregressive (or parallel/latent variable) generation of continuous-valued data. In this section, we will have a brief look into the two paradigms and give some examples of how they are modeled.
Autoregressive Generation#
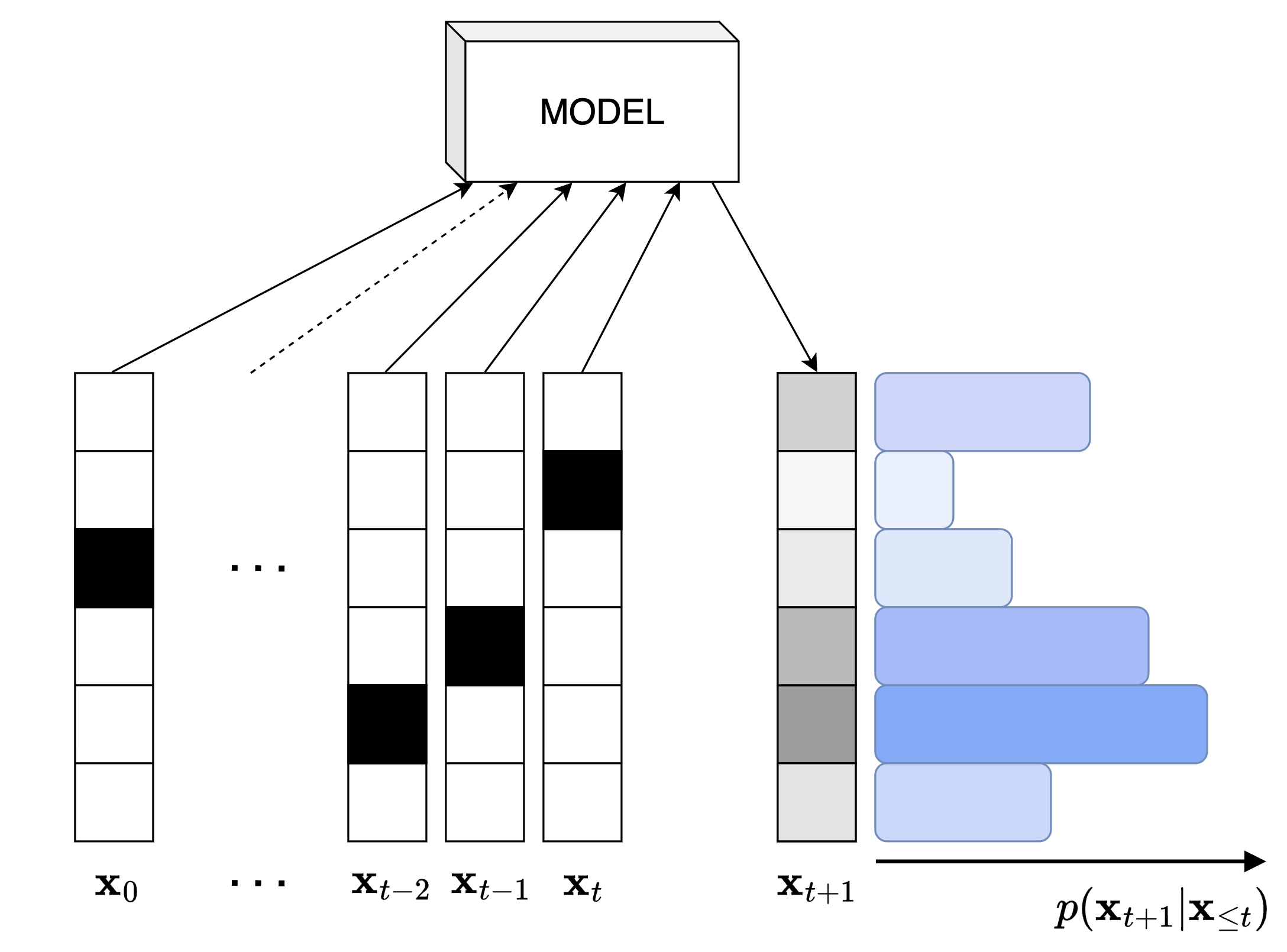
Figure 1: Schematic illustration of autoregressive generation. A sample \( \mathbf{x}_{t+1} \) is generated sequentially based on the conditional distribution \( p(\mathbf{x}_{t+1} | \mathbf{x}_{\leq t}) \), using all prior samples from the model.
For discrete sequences, models such as Recurrent Neural Networks (RNNs) [Elm90], Causal Convolutional Networks [vdODZ+16], and Transformers [VSP+17] are typically trained with cross-entropy loss to output a probability distribution over discrete random variables in a deterministic manner. The stochasticity is then “injected” by sampling from that distribution.
At each time step \(t\), the model outputs a probability distribution \(p(\mathbf{x}_t \mid \mathbf{x}_{<t})\) over the vocabulary \(V\), conditioned on the previous tokens \(x_{<t}\). The cross-entropy loss used during training can be expressed as:
where \(\mathbf{x}_t^*\) is the true token at time \(t\).
Note: In this case, we can primarily deal with one-hot encoded sequences, selecting one token per time step, as we don’t have a simple way to sample N-hot vectors (where \(N > 1\) tokens are selected simultaneously) from the model’s output distribution. Sampling multiple tokens at once would require modeling the joint probability of combinations of tokens, which significantly increases complexity and is not commonly addressed in standard sequence generation models.
Non-Autoregressive/Parallel/Latent Variable Generation#
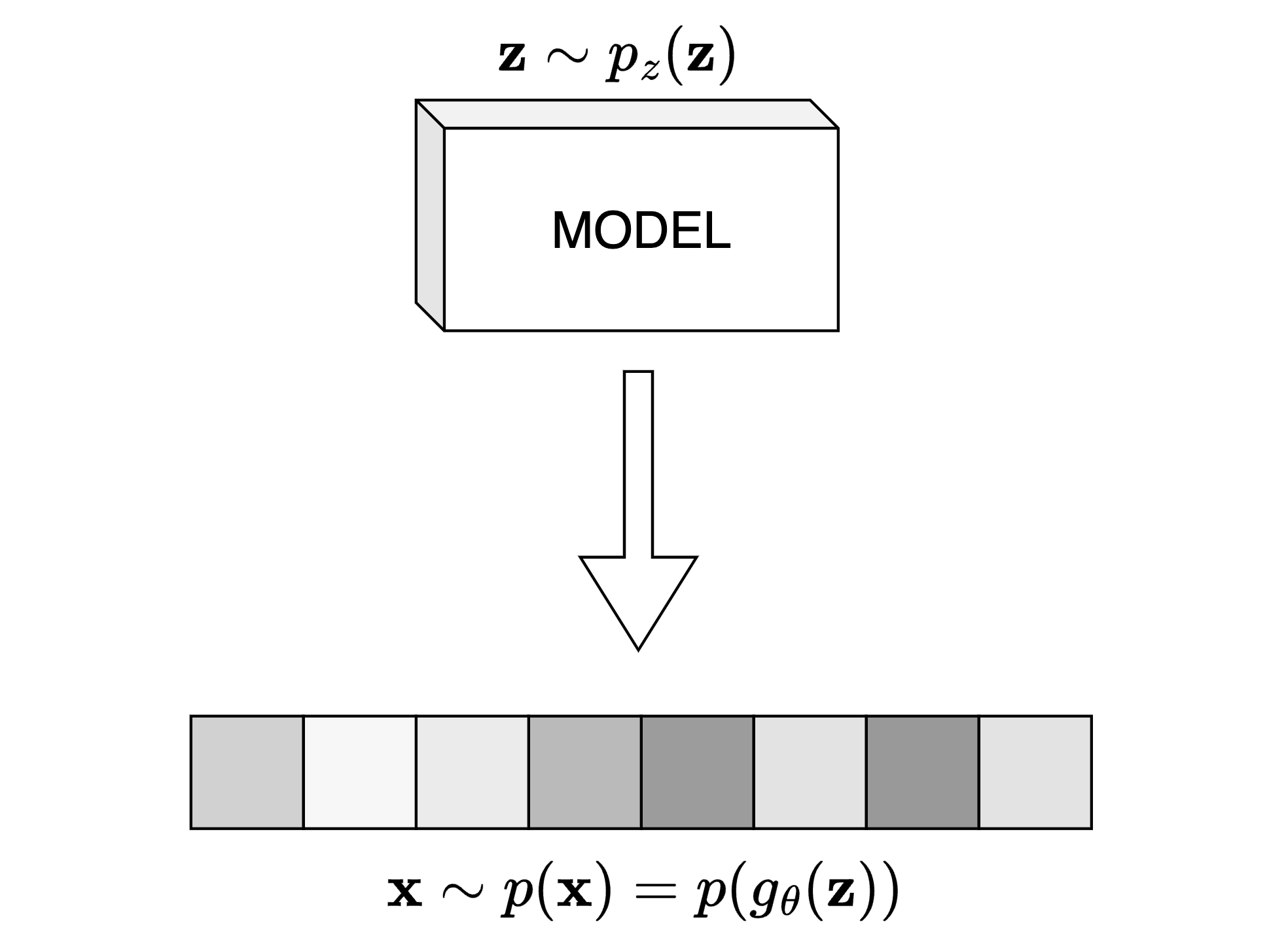
Figure 2: Schematic illustration of latent variable generation. A sample \( \mathbf{x} \) is generated by transforming \( \mathbf{z} \sim p_z(\mathbf{z}) \) through \( g_\theta \) to match the target distribution \( p(\mathbf{x}) \).
For generating continuous-valued data, the stochasticity usually comes from some form of noise injection into the neural network. Mathematically, this is typically defined as transforming a simple (usually Gaussian) distribution into the data distribution. In the following, a brief (architecture-agnostic) introduction in the most common training paradigms is given.
Generative Adversarial Networks (GANs)#
For example, Generative Adversarial Networks (GANs) [GPougetAbadieM+14] in their basic form inject noise by inputting a high-dimensional noise vector \(\mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\) (sampled from an independent Gaussian distribution) into the generator \(G\). The generator transforms this noise vector into a data sample: \(\mathbf{x} = G(\mathbf{z})\). Thus, the task can be described as learning to transform an independent Gaussian distribution into the data distribution.
The generator is trained by playing an adversarial game with a discriminator \(D\). The discriminator aims to distinguish between real samples from the dataset and fake samples generated by \(G\). The generator is trained to produce samples that maximize the likelihood of fooling the discriminator. This can be formalized by the minimax game between \(G\) and \(D\)
where \(p(\mathbf{z})\) represents the distribution of noise input. This adversarial setup ensures that as \(D\) improves in distinguishing real from fake data, \(G\) improves in generating more realistic samples, ultimately leading to convergence when the generated data becomes indistinguishable from the real data.
Variational Autoencoders (VAEs)#
Similarly, in Variational Autoencoders (VAEs, composed of encoder and decoder) [KW14], the decoder receives as input a sample from an independent Gaussian prior distribution (a “standard normal distribution”). The model is trained so that the encoder learns to approximate the prior using a mixture of Gaussian posteriors, one for each data point: \(\boldsymbol{\mu}, \boldsymbol{\sigma} = E(\mathbf{x})\), where \(\boldsymbol{\mu}\) and \(\boldsymbol{\sigma}\) are multi-dimensional mean and variance vectors. From this posterior, we sample a latent variable \(\mathbf{z} \sim q_{\phi}(\mathbf{z} \mid \mathbf{x}) = \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\sigma})\) during training. The decoder then reconstructs the input by transforming \(\mathbf{z}\) into a data point \(\hat{\mathbf{x}} = D(\mathbf{z})\).
Training involves minimizing two objectives: the reconstruction loss between \(\mathbf{x}\) and \(\hat{\mathbf{x}}\), and the Kullback-Leibler (KL) divergence between the learned posterior \(q_{\phi}(\mathbf{z} \mid \mathbf{x})\) and the prior distribution \(p(\mathbf{z}) \sim \mathcal{N}(0, I)\). The two objectives are adversarial because the KL term pushes the posteriors towards a zero mean and unit variance, while the reconstruction term encourages the posteriors to adopt distinct means and reduced variances, allowing each data point to have its own distribution. Together, they make it possible to sample from the prior \(p(\mathbf{z}) \sim \mathcal{N}(0, I)\) at inference and decoding it into a plausible data sample: \(\hat{\mathbf{x}} = D(\mathbf{z})\).
Diffusion Models#
In Diffusion Models [HJA20], the noise input has the same dimensionality as the data point that should be generated. The model gradually transforms noise into data through a series of steps. Like before, the goal is to transform a Gaussian prior distribution into the data distribution through the learned denoising steps. In its initial form it is defined as a Markov chain with learned Gaussian transitions starting at \(p(\mathbf{x}_T) = \mathcal{N}(\mathbf{x}_T; \mathbf{0}, \mathbf{I})\). The model learns to reverse the noising process by estimating \(p_{\theta}(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\):
