Cover Song Identification (CSI)#
Goal of CSI ?#
Cover(Version) Song Identification(Detection) is the task aiming at detecting if a given music track is a cover/version of an existing composition..
For example detecting that
this performance by Aretha Franklin
is a cover/version of the work-id “Let It Be”, composed by the Beatles and also performed in Beatles.
They are covers/versions of the same composition.
We said that they are performances of the same work-id (or ISWC).
The group of songs that are identified as cover versions of each other is often denoted as a “clique”.
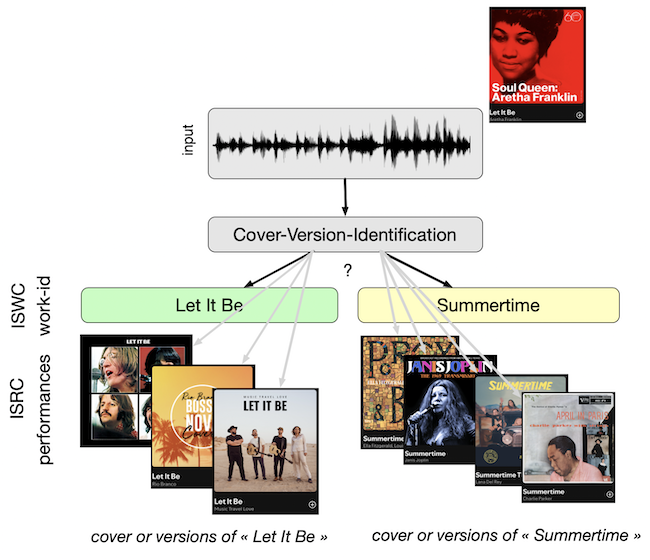
Common approach#
Considering the very large number of possible work-id (there exist millions of compositions), it is not possible to solve this as a classification (multi-class) problem (too many classes).
To solve this, the approach commonly used is to
have a a reference dataset \(R\), containing tracks \(\{r_i\}\) with known work-id,
compare the query track \(q\) to each track \(r_i\) of the reference dataset.
If \(q\) is similar to one track of the dataset (i.e. the distance \(d(q,r_i)\) is small),
\(\Rightarrow\) we decide that \(q\) is a cover of \(r_i\) and they share the same work-id.
This involves setting a threshold \(\tau\) on \(d(q,r_i)\). If \(d(q,r_i)<\tau\) we decide they are cover of each other.
A very short history of CSI#
The story starts with Ellis et al. [EP07] who proposed to compute \(d(q,r_i)\) as the cross-correlation between processed Chroma/PCP features of \(q\) and \(r_i\).
Later on, Serra et al. [SerraGomez08] proposed to improve the features (Harmonic-PCP) and the comparison algorithm (DTW, Dynamic Time Warping). This has lead to the standard approach for years. However, computing the DTW for every pair of tracks is computationally expensive.
To reduce the cost, \(d\) should simplified to a simple Euclidean distance between trained features/embedding extracted from \(q\) and \(r_i\). Such an approach have been tested in the linear case (using 2D-DFT, PCA, ..) by [HNB13]. However, the results were largely below those of Serra.
Deep learning era.
The solution will come from Computer Vision and the face recognition problem in which deep learning is used to perform metric learning [SKP15].
This method will be transferred to do the cover-song-identification case by [DP19] and [YSerraGomez20].
Fore more details, see the very good tutorial “Version Identification in the 20s”.
How is CSI evaluated ?#
In practice to evaluate the task, another problem is considered.
The distances between \(q\) and all \(r_i \in R\) are computed and ranked (from the smallest to the largest) \(\Rightarrow A\)
we denote by \(w(.)\) the function that gives the work-id of a track,
we check at which position in the ranked list \(A\) we have \(w(r_i \in A)==w(q)\).
We can then use the standard ranking/recommendation performance metrics.
If we denote by
\(A\) the ranked list (of length \(K\)) corresponding to a query \(q\)
\(a_i\) its \(i^{th}\) element,
\(A^k=\{a_i\}_{i \; \in \; 1 \ldots k}\) the \(k\) first ranked items,
\(rel(q,a_i)\) the relevance of items \(a_i\), i.e. whether the item \(a_i\) has the same work-id than \(q\): \(w(a_i)==w(q)\).
We then compute the usual ranking metrics:
MR1: Mean Rank (lower better): it is the mean (average over queries) of the rank of the first correct result
\(\hspace{3cm} MR1=\mathbb{E}_{q \in Q} \arg\min_i \{ rel(q,a_i)=1 \}\)MRR1: Mean Reciprocal Rank (higher better): it is the mean (…) of 1/rank of the first correct result
\(\hspace{3cm} MRR1=\mathbb{E}_{q \in Q} \arg\max_i \frac{1}{ rel(q,a_i)=1}\)Precision @ k (higher better): the number of correct results in the first \(k\) elements of the ranked list
\(\hspace{3cm} P(k) = \frac{1}{k} \sum_{i=1}^k rel(q,a_i)\)mAP: mean Average Precision (higher better): same as for multi-label classification
\(\hspace{3cm} AP^q = \frac{1}{K} \sum_{k=1}^K P(k) \; rel(q,a_k)\)

def F_mean_rank(relevance):
return relevance.nonzero()[0][0]+1
def F_mean_reciprocal_rank(relevance):
return 1./ F_mean_rank(relevance)
def F_precision_at_k(relevance, k):
return np.mean(relevance[:k] != 0)
def F_average_precision(relevance):
out = [F_precision_at_k(relevance, k + 1) for k in range(relevance.size) if relevance[k]]
return np.mean(out)
Other metrics are also commonly used such as the Cumulative Gain, (CG) Discounted Cumulative Gain (DCG), Normalised DCG.
Some popular datasets for CSI#
A (close to) exhaustive list of MIR datasets is available in the ismir.net web site.
The first dataset proposed for this task was the cover80 datasets containing 80 different work-id (or cliques) with 2 versions each.
Since then, much larger datasets have been created mostly relying on the data provided by the collaborative website SecondHandSongs.
For our implementations, we will consider the two following datasets:
Cover-1000: 996 performances of 395 different works
DA-TACOS: 15.000 performances of 3000 different works
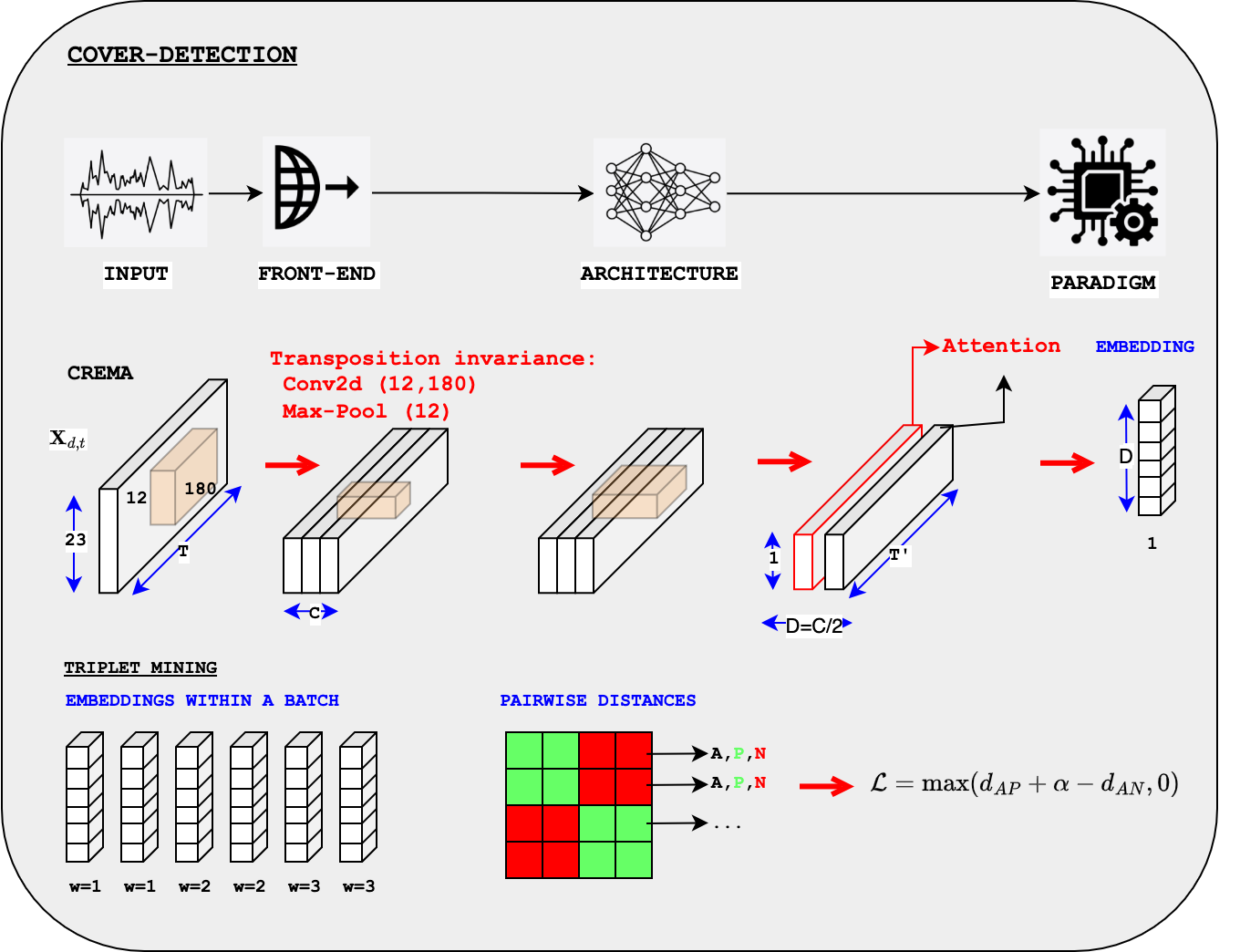
Notes that those do not provide access to the audio but to the already extracted CREMA features [MB17] (12-dimensional).
How can we solve CSI using deep learning ?#
The usual deep learning technique is based on metric learning:
we train a neural network \(f_{\theta}\) such that the projections of \(q\), \(f_{\theta}(q)\) can be directly compared (using Euclidean distance) to the projections of \(r_i\), \(f_{\theta}(r_i)\).
the distance should relates to their “cover-ness” (how much \(q\) and \(r_i\) are two performances of the same work-id).
only the projections (named embedding) of the elements of the reference-set \(R\) are stored
Various approaches can be used for metric learning, but the most common is the triplet loss.
For the proposal code we will used the MOVE model [YSerraGomez20] and follow its implementation.
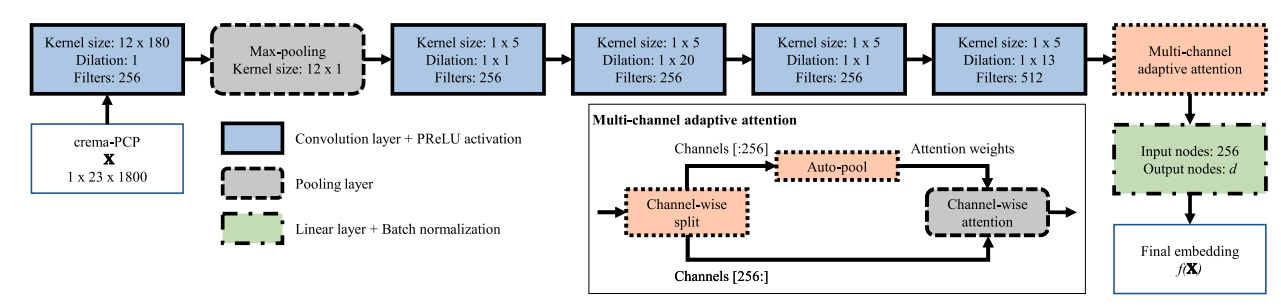
Figure MOVE model for CSI proposed by [YSerraGomez20]
We test the results on two datasets:
a small one (Cover-1000)
a large one (DA-TACOS-benchmark)
Experiments#
The code is available here:
(Main notebook)(geoffroypeeters/deeplearning-101-audiomir_notebook)
(Config Cover)[geoffroypeeters/deeplearning-101-audiomir_notebook]
Dataset |
Input |
Frontend |
Results |
Code |
|---|---|---|---|---|
Cover1000 |
CREMA |
Move |
meanRank=11.2, meanRecRank=0.551, P@1=0.44, mAP=0.11 |
|
Datacos-benchmark |
CREMA |
Move |
meanRank=465.3, meanRecRank=0.201, P@1=0.13, mAP=0.073 |
Code:#
Illustrations of
show config Model, explain invariance to transposition (maxpool-12)
show
CoverDataset, explain__getitem__provides a click,train_dataloaderprovides a set of work-idexplain AutoPoolWeightSplit
explain Online Triplet Mining,
triplet_loss_miningshow performance measures, evaluation of number of OK triplets
Online Triplet mining explained#
The online mining of the triplets is actually not a mining of the best data to be fed to the model since all data are actually fed into the model to obtain the embeddings:
Online mining is the mining of the subset of \(\mathbf{e}_i\) that will be used in the loss.
Online mining select the \(\{( \mathbf{e}_i \}\) that will form the triplets
{A,P,N}which are then used to compute the loss (which is to be minimized by SGD).Only those selected are used for the loss.
Distance matrix#
We first compute a pair-wise distance matrix dist_all between all the embeddings \(\mathbf{e}_i\).
The “cliques” are grouped together in the matrix, i.e. the performances \(\{i-1, i, i+1\}\) belong to the same work-id.
We can then create
a
mask_pos: all the distances of similar work-ida
mask_neg: all the distances of different work-id
Random mining#
For each anchor A (row), we select randomly a positive (among the mask_pos) and a negative (among the mask_neg).
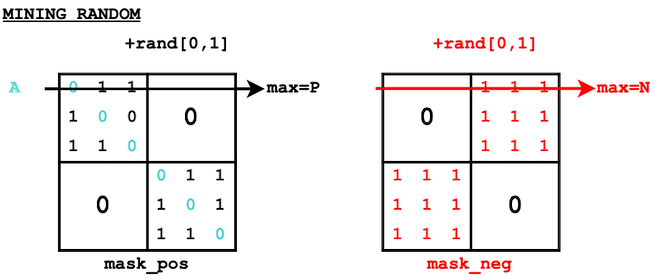
def triplet_mining_random(dist_all, mask_pos, mask_neg):
"""
Performs online random triplet mining
"""
# selecting the positive elements of triplets
# we consider each row as an anchor and takes the maximum of the masked row (mask_pos) as the positive
_, sel_pos = torch.max(mask_pos.float() + torch.rand_like(dist_all), dim=1)
dists_pos = torch.gather(input=dist_all, dim=1, index=sel_pos.view(-1, 1))
# selecting the negative elements of triplets
# we consider each row as an anchor and takes the maximum of the masked row (mask_neg) as the negative
_, sel_neg = torch.max(mask_neg.float() + torch.rand_like(dist_all), dim=1)
dists_neg = torch.gather(input=dist_all, dim=1, index=sel_neg.view(-1, 1))
return dists_pos, dists_neg
Semi-hard mining#
For each anchor A (row), we select randomly a positive (among the mask_pos) and a negative (among the mask_neg that statisfy D_neg < D_pos + margin).
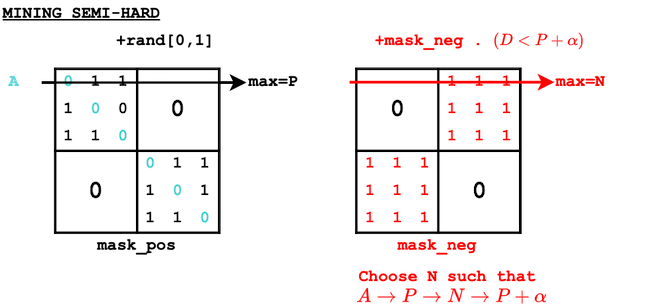
def triplet_mining_semihard(dist_all, mask_pos, mask_neg, margin):
"""
Performs online semi-hard triplet mining (a random positive, a semi-hard negative)
"""
# --- the code below seems wrong
# --- need criteria
# 1) should be negative (should be from a different work-id)
# 2) should be P < N < P+margin
# selecting the positive elements of triplets
# we consider each row as an anchor and takes the maximum of the masked row (mask_pos) as the positive
_, sel_pos = torch.max(mask_pos.float() + torch.rand_like(dist_all), dim=1)
dists_pos = torch.gather(input=dist_all, dim=1, index=sel_pos.view(-1, 1))
# selecting the negative elements of triplets
_, sel_neg = torch.max(
(mask_neg
+ mask_neg * (dist_all < (dists_pos.expand_as(dist_all)).long()+margin)).float()
+ torch.rand_like(dist_all),
dim=1)
dists_neg = torch.gather(input=dist_all, dim=1, index=sel_neg.view(-1, 1))
return dists_pos, dists_neg
Hard mining#
For each anchor A (row), we select (among the mask_pos) the positive with the largest distance and the negative (among the mask_neg) with the smallest distance.
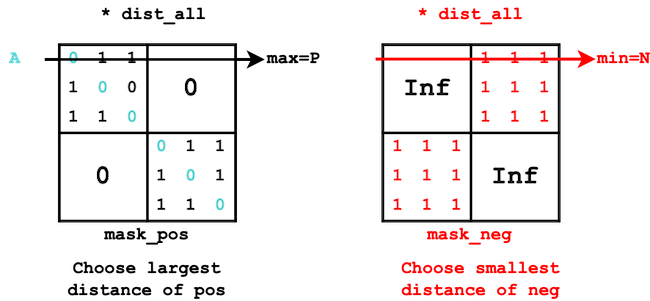
def triplet_mining_hard(dist_all, mask_pos, mask_neg, device):
"""
Performs online hard triplet mining (both positive and negative)
"""
# --- the code below seems wrong
# --- need criteria
# 1) should be negative (from a different work-id)
# 2) should be N < P
# selecting the positive elements of triplets
# --- for each anchor (row) we take the positive with the largest distance
_, sel_pos = torch.max(dist_all * mask_pos.float(), 1)
dists_pos = torch.gather(input=dist_all, dim=1, index=sel_pos.view(-1, 1))
# modifying the negative mask for hard mining (because we will use the min)
# --- if mask_neg==0 then inf
# --- if mask_neg==1 then 1
true_value = torch.tensor(float('inf'), device=device)
false_value = torch.tensor(1., device=device)
mask_neg = torch.where(mask_neg == 0, true_value, false_value)
# selecting the negative elements of triplets
# --- for each anchor (row) we take the negative with the smallest distance
_, sel_neg = torch.min(dist_all + mask_neg.float(), dim=1)
dists_neg = torch.gather(input=dist_all, dim=1, index=sel_neg.view(-1, 1))
return dists_pos, dists_neg
