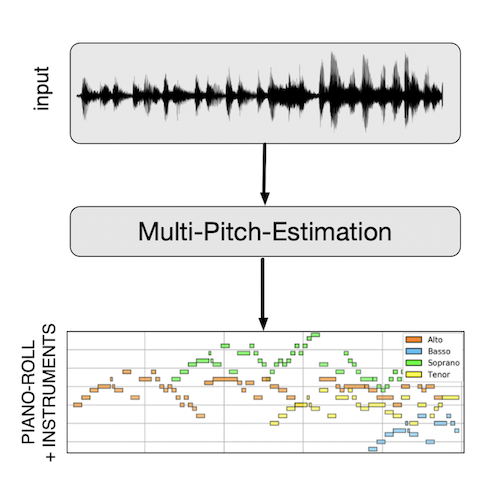
Multi-Pitch-Estimation (MPE)#
Goal of MPE ?#
Multi-Pitch-Estimation aims at extracting information related to the simultaneously occuring pitches over time within an audio file. The task can either consists in:
estimating at each time frame the existing continuous fundamental frequencies (in Hz): \(f_0(t)\)
estimating the [start_time, end_time, pitch] of each musical note (expressed as MIDI note)
assigning an instrument-name (source) to the above(see illustration)
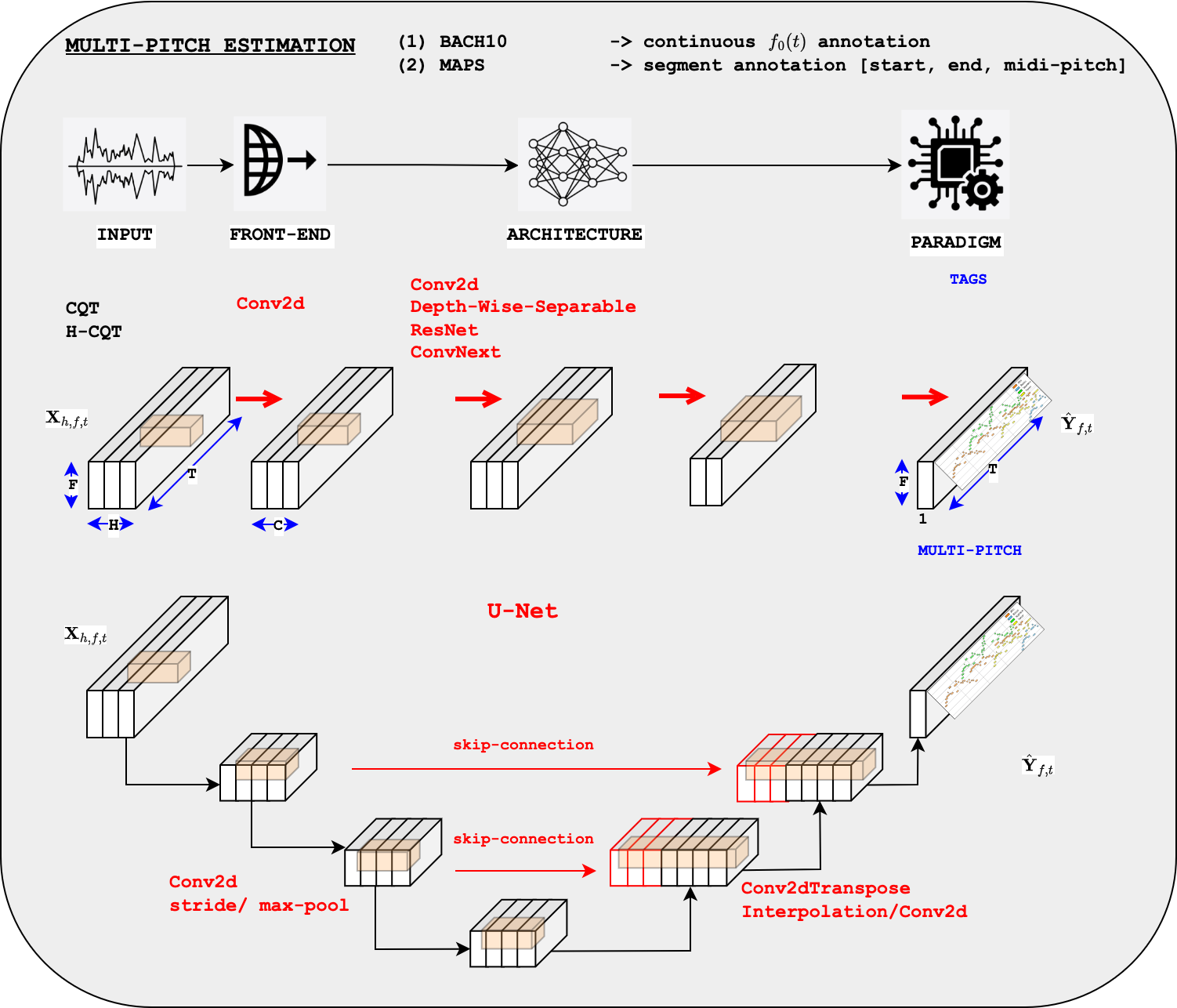
A very short history of MPE#
The task has a long history.
Early approaches focused on single pitch estimation (SPE) using a signal-based method, such as the YIN [DK02] algorithm.
Next, the difficult case of multiple pitch estimation (MPE) (overlapping harmonics, ambiguous number of simultaneous pitches) was addressed using iterative estimation, as in Klapuri et al [Kla03].
Subsequently, the main trend has been to use unsupervised methods aiming at reconstructing the signal using a mixture of templates (with non-negative matrix factorisation NMF, probabilistic latent component analysis PLCA or shift-invariant SI-PLCA) [FBR13].
Deep learning era.
We review here one of the most famous approaches proposed by Bittner et al [BMS+17]
We show how we can extend it with the same front-end (Harmonic-CQT) using a U-Net [DEP19, WP22].
The task is still very active today, especially using unsupervised learning approaches, more specifically the ”equivariance” property, such as in SPICE [GFR+20] or PESTO [RLHP23]
Fore more details, see the very good tutorials “Fundamental Frequency Estimation in Music” and “Programming MIR Baselines from Scratch: Three Case Studies”.
How is MPE evaluated ?#
To evaluate the performances of an MPE algorithm we rely on the metrics defined in [BED09] and implemented in the mir_eval package. By default, an estimated frequency is considered ”correct” if it is within 0.5 semitones of a reference frequency.
Using this, we compute at each time frame t:
”True Positives” TP(t): the number of \(f_0\)’s detected that correctly correspond to the ground-truth \(f_0\)’s
”False Positives” FP(t): the number of \(f_0\)’s detected that do not exist in the ground-truth set
”False Negatives” FN(t): represent the number of active sources in the ground-truth that are not reported
From this, one can compute
Precision= \(\frac{\sum_t TP(t)}{\sum_t TP(t)+FP(t)}\)
Recall= \(\frac{\sum_t TP}{\sum_t TP(t)+FN(t)}\)
Accuracy= \(\frac{\sum_t TP(t)}{\sum_t TP(t)+FP(t)+FN(t)}\)
We can also compute the same metrics but considering only the chroma associated to the estimated pitch (independently of the octave estimated).
This leads to the Chroma Precision, Accuracy, Recall.
Example:
freq = lambda midi : 440*2**((midi-69)/12)
ref_time = np.array([0.1, 0.2, 0.3])
ref_freqs = [np.array([freq(70), freq(72)]), np.array([freq(70), freq(72)]), np.array([freq(70), freq(72)])]
est_time = np.array([0.1, 0.2, 0.3])
est_freqs = [np.array([freq(70.4+12)]), np.array([freq(70), freq(72), freq(74)]), np.array([freq(70), freq(72)])]
mir_eval.multipitch.evaluate(ref_time, ref_freqs, est_time, est_freqs)
OrderedDict([('Precision', 0.6666666666666666),
('Recall', 0.6666666666666666),
('Accuracy', 0.5),
('Substitution Error', 0.16666666666666666),
('Miss Error', 0.16666666666666666),
('False Alarm Error', 0.16666666666666666),
('Total Error', 0.5),
('Chroma Precision', 0.8333333333333334),
('Chroma Recall', 0.8333333333333334),
('Chroma Accuracy', 0.7142857142857143),
('Chroma Substitution Error', 0.0),
('Chroma Miss Error', 0.16666666666666666),
('Chroma False Alarm Error', 0.16666666666666666),
('Chroma Total Error', 0.3333333333333333)])
Some popular datasets for MPE#
A (close to) exhaustive list of MIR datasets is available in the ismir.net web site.
MPE datasets can be obtained in several ways:
annotating manually the full-tracks,
annotating (manually or automatically using SPE) the individual stems of a full-track: such as Bach10 or MedleyDB
using audio to score synchronization: such as MusicNet, SMD or SWD
We have chosen the two following datasets since they represent two different types of annotations:
Bach10#
Bach10 [DPZ10] is a small (ten tracks) but multi-track datasets in which each track is annotated in pitch (time, continuous f0-value) over time-frames.
"entry": [
{
"filepath": [
{"value": "01-AchGottundHerr-violin.wav"}
],
"f0": [
{"value": [
[
72.00969707905834,
72.00969707905834,
72.00763743216136,
72.00763743216136,
72.00763743216136,
72.03300373636725,
72.04641885597061,
...
]
]}
{"time": [
0.023,
0.033,
0.043,
0.053,
0.063,
0.073,
0.083,
...
]}
ENST MAPS#
ENST MAPS (MIDI Aligned Piano Sounds) [EBD10] is a large (31 Go) piano dataset. Four categories of sounds are provided: isolated notes, random chords, usual chords, pieces of music. We only use the later for our experiment. It is annotated as a sequence of notes (start,stop,midi-value) over time.
This dataset has been made available online with Valentin Emiya’s permission specifically for this tutorial. For any other use, please contact Valentin Emiya to obtain authorization.
"entry": [
{
"filepath": [
{"value": "MAPS_MUS-alb_se3_AkPnBcht.wav"}
],
"pitchmidi": [
{"value": 67, "time": 0.500004, "duration": 0.26785899999999996},
{"value": 71, "time": 0.500004, "duration": 0.26785899999999996},
{"value": 43, "time": 0.500004, "duration": 1.0524360000000001},
...
]
}
How can we solve MPE using deep learning ?#
We propose here a solution for the MPE task using supervised learning, i.e. with known output y.
Rather than estimating the continuous \(f_0\) by regression, we consider the classification problem into pitch-classes (\(f_0\) are quantized to their nearest semi-tone or \(\frac{1}{5}^{th}\) of semi-tone)
The output
yto be predicted is a binary matrix \(\mathbf{Y} \in \{0,1\}^{(P,T)}\) indicating the presence of all possible pitch-classes \(p\in P\) over time \(t \in T\)The problem is then a supervised multi-label problem
\(\Rightarrow\) We use a set sigmoids and Binary-Cross-Entropys
For the input X, we study various choices
the CQT
the Harmonic-CQT proposed by [BMS+17].
For the model \(f_{\theta}\), we study various designs
variations of its blocks: Depthwise Separable Convolution, ResNet, ConvNext
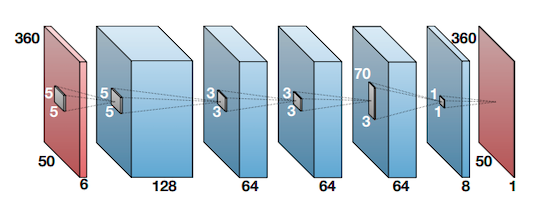
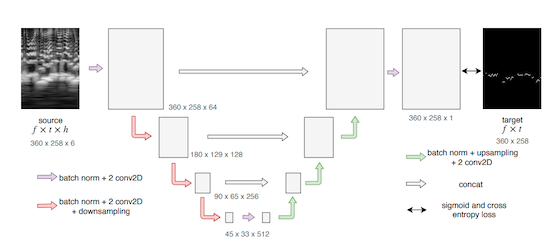
the U-Net model proposed by [DEP19, WP22] (see Figure below)
Conv-2D model for MPE |
U-Net model for MPE |
|---|---|
|
|
Figure proposed by [BMS+17] |
We test the results on two datasets:
a small one (Bach10 with continous f0 annotation)
a large one (MAPS with segments annotated in MIDI-pitch)
Experiments#
The code is available here:
(Main notebook)(geoffroypeeters/deeplearning-101-audiomir_notebook)
(Config Conv2D)[geoffroypeeters/deeplearning-101-audiomir_notebook]
(Config U-Net)[geoffroypeeters/deeplearning-101-audiomir_notebook]
Dataset |
Input |
Frontend |
Results |
Code |
|---|---|---|---|---|
Bach10 |
CQT(H=1) |
Conv2D |
P=0.84, R=0.71, Acc=0.63 |
|
Bach10 |
HCQT(H=6) |
Conv2D |
P=0.92, R=0.79, Acc=0.74 |
|
Bach10 |
HCQT(H=6) |
Conv2D/DepthSep |
P=0.92, R=0.78, Acc=0.74 |
|
Bach10 |
HCQT(H=6) |
Conv2D/ResNet |
P=0.93, R=0.80, Acc=0.75 |
|
Bach10 |
HCQT(H=6) |
Conv2D/ConvNext |
P=0.92, R=0.80, Acc=0.75 |
|
Bach10 |
HCQT(H=6) |
U-Net |
P=0.91, R=0.78, Acc=0.73 |
|
– |
– |
– |
– |
– |
MAPS |
HCQT(H=6) |
Conv2D |
P=0.86, R=0.75, Acc=0.67 |
|
MAPS |
HCQT(H=6) |
Conv2D/ResNet |
P=0.83, R=0.83, Acc=0.71 |
|
MAPS |
HCQT(H=6) |
U-Net |
P=0.84, R=0.81, Acc=0.70 |
Code:#
Illustrations of
show config Conv2D
show code Bach10/HCQT/Conv2D
f_parrallel
f_map_annot_frame_based
PitchDataset
Check the model
PitchLigthing, EarlyStopping, ModelCheckpoint, trainer.fit
Evaluation: load_from_checkpoint, illustration, mir_eval, plot np.argmin
show config U-Net
show code ResNet on MAP