Inputs

We denote by input the \(\textbf{X}\) fed to a neural network. We describe in the following the usual type of inputs in the case of audio.

Waveform

It is possible to use directly the audio waveform \(\mathbf{x}_n\) as input to a model. In this case, the input is a 1-dimensional sequence over time. Such a system is often denoted by end-to-end (E2E). The first layer of the models then act as a learnable feature extractor. It is often either a 1D-convolution, a TCN or a parametric front-end such as SincNet.

More details can be found in the following “Waveform-based music processing with deep learning” by Jongpil Lee, Jordi Pons, Sander Dieleman ISMIR-2019 tutorial.

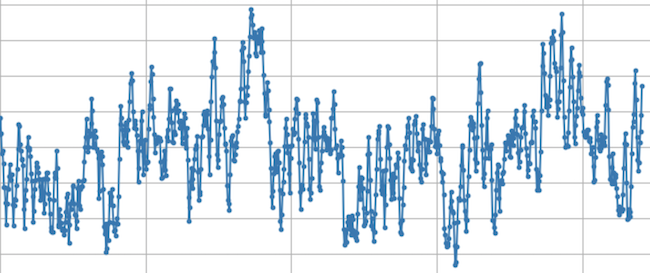
Figure Waveform of an audio signal with sample values.

Log-Mel-Spectrogram (LMS)

The spectrogram \(|\mathbf{X}_{k,m}|\) is the magnitude of the Short Time Fourier Transform of the signal \(\mathbf{x}_n\) with

• discrete frequencies \(k\) and

• time frames \(m\)

Its frequencies can be converted to the Mel perceptual scale. This allows

• to reduce the dimensionality of the data

• to mimic the decomposition of the frequencies performed by the cochlea into critical-bands

• to allows performing (some) invariance over small pitch modifications (

  • hence LMS are invariant to the pitch and only represent the so-called timbre.

Its amplitude can be concerted to the Log-scale. This allows

• to map the recording level of the audio to a constant: \(\alpha \mathbf{x}_n \rightarrow \log(\alpha) + \log(\mathbf{X}_{k,m})\)

• to mimic the compression of the amplitude performed by the inner-cell of the cochlea

• to change the distribution of the input

Usually, a \(\log(1+C x)\) (with \(C=10.000\)) is used instead of a \(\log(x)\) to avoid singularity in \(x=0\).

Another explanation of the LMS, is to consider that those are equivalent to the MFCC but without the last DCT performed for the MFCC. Indeed this DCT was necessary to decorrelate the dimensions and then allows covariance matrix in GMM-based systems but is not necessary for deep learning models.

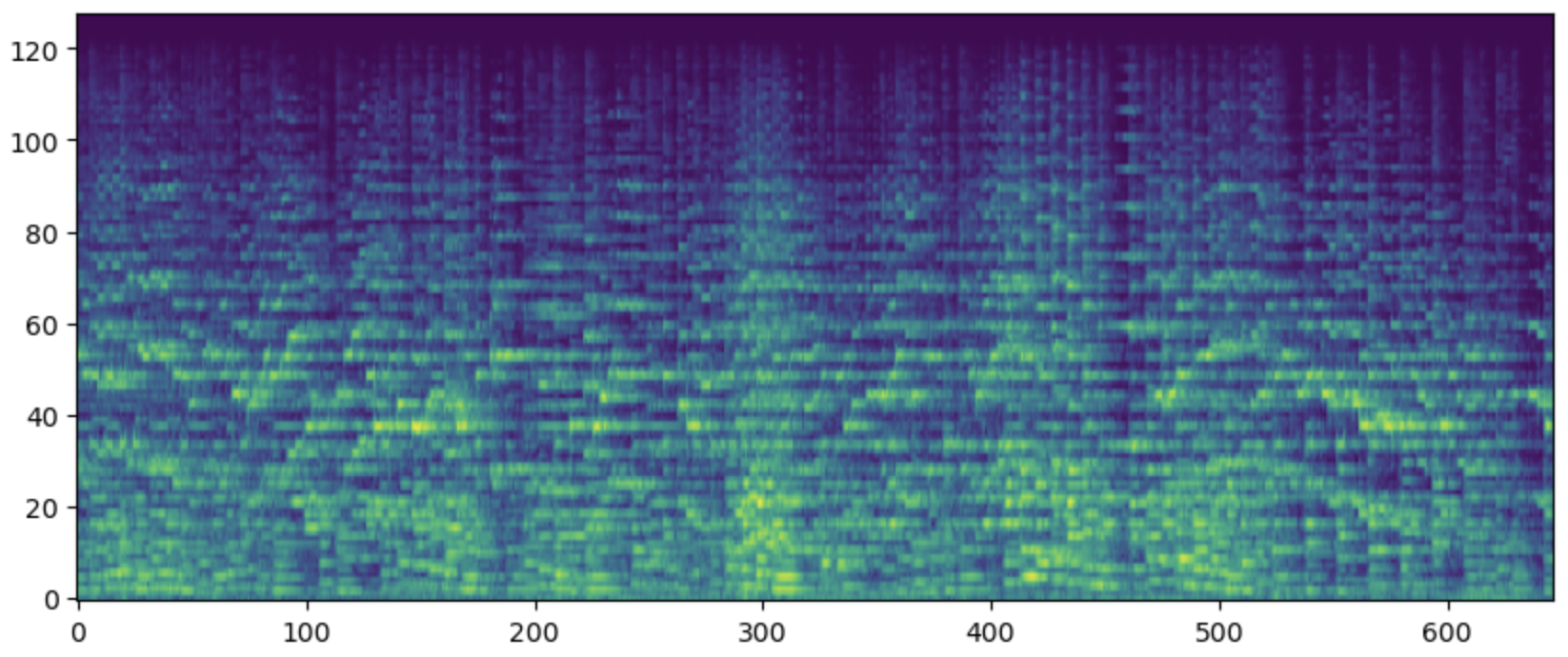
Figure Log-Mel-Spectrogram of an audio signal with 128 Mel bands.

def f_get_lms(audio_v, sr_hz, param_lms):
    """
    description:
        compute Log-Mel-Sepctrogram audio features
    inputs:
        - audio_v
        - sr_hz
    outputs:
        - data_m (nb_dim, nb_frame): Log-Mel-Spectrogram matrix
        - time_sec_v (nb_frame): corresponding time [in sec] of analysis windows
    """
    # --- data (nb_dim, nb_frames)
    mel_data_m = librosa.feature.melspectrogram(y=audio_v, sr=sr_hz,
                                                n_mels=param_lms.nb_band,
                                                win_length=param_lms.L_n,
                                                hop_length=param_lms.STEP_n)
    data_m = f_log(mel_data_m)
    nb_frame = data_m.shape[1]
    time_sec_v = librosa.frames_to_time(frames=np.arange(nb_frame),
                                        sr=sr_hz,
                                        hop_length=param_lms.STEP_n)

    return data_m, time_sec_v

Constant-Q-Transform (CQT)

Constant-Q-Transform was proposed in [Bro91].

• The CQT divides the frequency axis into bins where the ratio between adjacent frequencies is constant (i.e., logarithmically spaced): \(r=f_{k+1}/f_k=cst\)

  • This is different from the Discrete Fourier Transform (DFT), where frequency bins are linearly spaced \(f_{k+1}-f_k = cst\).

  • In music \(r=2^{1/12}\) for adjacent musical pitches (semitones).

  • It is possible to increase the number of bins for each semitone (if 5 bins per semitone the ratio is \(r=2^{1/(5 \cdot 12)}\))

• The CQT adapts the duration of the analysis window \(\mathbf{w}_k\) for each frequency \(f_k\), in order to be able to spectrally separate adjacent frequencies \(f_k, f_{k+1}\).

  • This is different from the DFT, which uses a single analysis window \(\mathbf{w}\) (hence a single duration) for all its frequencies \(f_k\) (hence with a fixed spectral resolution),

Because of the frequencies are expressed in log-scale in the CQT, pitch-shifting of a musical instrument correspond to a vertical translation of the corresponding CQT (\(\alpha f \rightarrow \log(\alpha) + \log(f)\). This property has been used in some works such as Shift-Invariant PLCA or in 2D-Convolution.

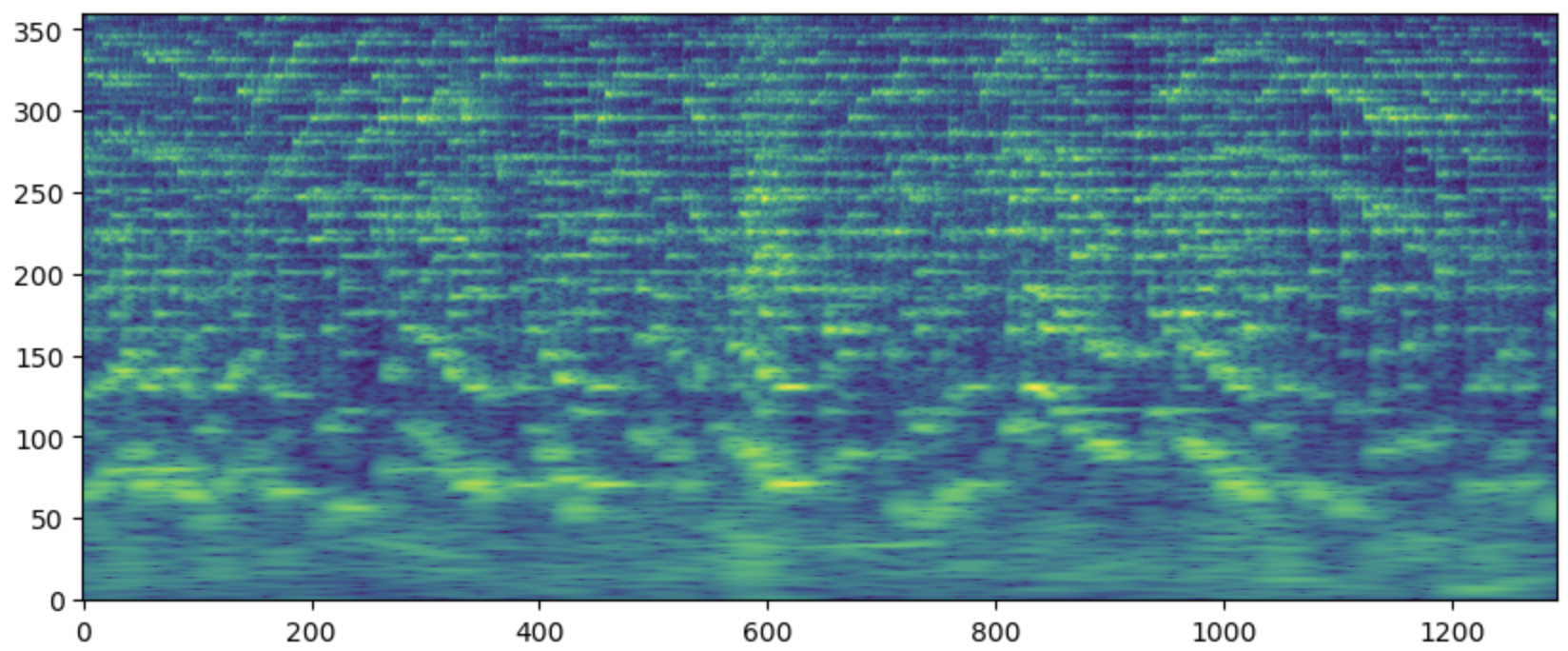
Figure Constant-Q-Transform of an audio signal with 6 octaves and 5 bins per semi-tone (\(6 \times 12 \times 5\) frequencies).

Harmonic-CQT (HCQT)

The Harmonic-CQT has been proposed in [BMS+17].

• The usual ”local correlation of the pixels” assumption underlying 2D-Convolution does not hold for musical sound. This is because the harmonics \(h f_0\) of a given sound are spread over the whole spectrum, hence the content at frequencies \(f_k\) are not correlated.

• To allow highlighing this correlation of harmonics, the Harmonic-CQT represent the harmonics of a frequency \(f_k\) in a new depth/channel dimension

  • In this, a channel \(h\) represent the frequencies \(f^{(h)}_k = h f_k\)

    • Using channels \(h \in \{1,2,3,4,5\}\) allows to represent in the depth the first five harmonics of a potentially pitched sound at \(f_0=f_k\): \(f^{(1)}_k = f_k, f^{(2)}_k = 2 f_k, f^{(3)}_k = 3 f_k, \ldots \)

  • To compute it, we use CQTs with different starting frequencies \(h f_{min}\)

  • The HCQT is obtained by stacking the various downsampled CQTs in depth/channel dimension

  • The resulting Harmonic-CQT is a 3D-tensorof dimensions (harmonic, time, frequencies).

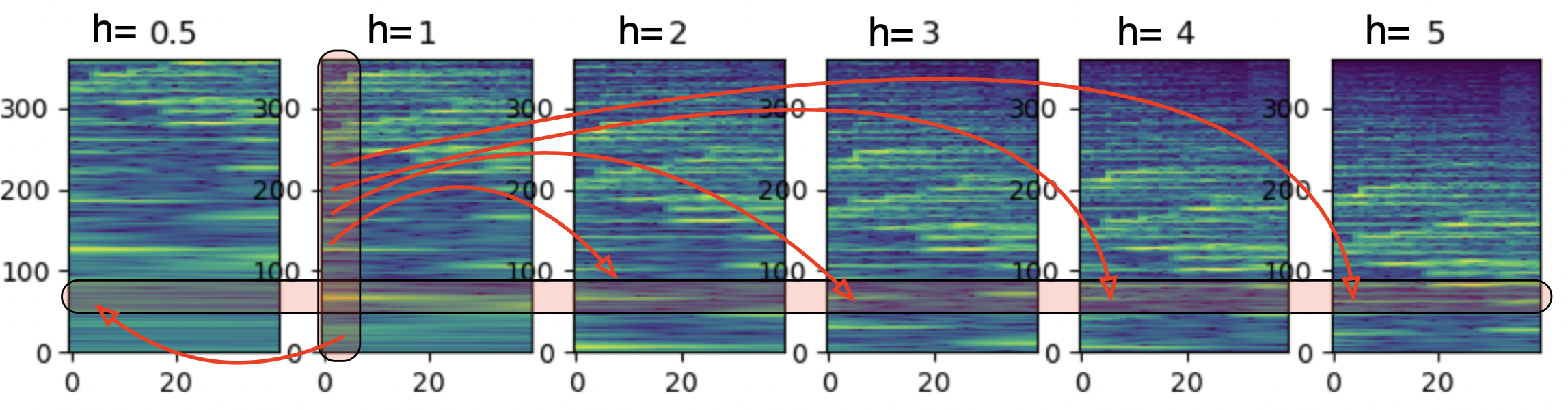Figure Set of CQT of the same audio signal with various starting frequencies \(f_{min}\). The default CQT is referred as “h=1”. The red vertical stripe highlight the fundamental frequency of a sound. In \(h=1\), the stripe highlights \(f_0\). If we downsample the CQT by a factor 2 (indicated in “h=2”), the stripe now highlight \(2 f_0\). If we downsample the CQT by a factor 3 (indicated in “h=3”), the stripe now highlight \(3 f_0\). The various harmonics \(h f_0\) are now aligned vertically across downsampled versions.

The HCQT is often used as input to a 2D-Convolution layer with small kernels \((5 \times 5)\) which extend over the whole depth of the HCQT. When used for Multi-Pitch-Estimation, the kernels should therefore learn the specific relationship among harmonics specific to harmonics versus non-harmonics. An extra component \(h=0.5\) is added to avoid octave errors.

Figure 2D-Convolution (over time and frequencies) of the HCQT with \((5 \times 5)\) kernels which extend over the whole depth.

def f_get_hcqt(audio_v, sr_hz, param_hcqt):
    """
    description:
        compute Harmonic CQT
    inputs:
        - audio_v
        - sr_hz
    outputs:
        - data_3m (H, nb_dim, nb_frame): Harmonic CQT
        - time_sec_v (nb_frame): corresponding time [in sec] of analysis windows
        - frequency_hz_v (nb_dim): corresponding frequency [in Hz] of CQT channels
    """
    for idx, h in enumerate(param_hcqt.h_l):
        A_m = np.abs(librosa.cqt(y=audio_v, sr=sr_hz,
                                fmin=h*param_hcqt.FMIN,
                                hop_length=param_hcqt.HOP_LENGTH,
                                bins_per_octave=param_hcqt.BINS_PER_OCTAVE,
                                n_bins=param_hcqt.N_BINS))
        if idx==0:
            data_3m = np.zeros((len(param_hcqt.h_l), A_m.shape[0], A_m.shape[1]))
        data_3m[idx,:,:] = A_m

    n_times = data_3m.shape[2]
    time_sec_v = librosa.frames_to_time(np.arange(n_times),
                                            sr=sr_hz,
                                            hop_length=param_hcqt.HOP_LENGTH)
    frequency_hz_v = librosa.cqt_frequencies(n_bins=param_hcqt.N_BINS,
                                                    fmin=param_hcqt.FMIN,
                                                    bins_per_octave=param_hcqt.BINS_PER_OCTAVE)

    return data_3m, time_sec_v, frequency_hz_v

Chroma/ Pitch-Class-Profile

Chroma (or Pitch-Class-Profile) [Fuj99] [Wak99] is a compact (12-dimensions) representation of the harmonic content over time of a music track.

• Its dimensions correspond to the pitch-classes (hence independently of their octave): C, C#, D, D#, E, …

• Chroma can be obtained by mapping the content of the spectrogram (or the CQT) to the pitch-classes (summing the content of all frequency bands corresponding to the C0, C1, C2, … to obtain the Chroma C, …).

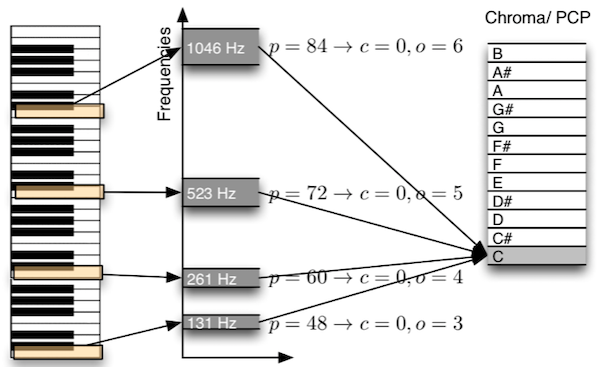
Figure Chroma map the content of the DFT frequencies to the 12 semi-tones pitch-classes

librosa.feature.chroma_stft(*, y=None, sr=22050, S=None, norm=inf, n_fft=2048, hop_length=512, win_length=None, window='hann', center=True, pad_mode='constant', tuning=None, n_chroma=12)
librosa.feature.chroma_cqt(*, y=None, sr=22050, C=None, hop_length=512, fmin=None, norm=inf, threshold=0.0, tuning=None, n_chroma=12, n_octaves=7, window=None, bins_per_octave=36)

Since the direct mapping from spectram/CQT suffers from artifacts (fifth harmonics, noise, percussive instruments), it has been proposed to learn a cleaner chroma representation using deep learning models, the so-called deep-chroma [KW16] [MB17] [WP21].

Chroma are often as input for applications such as Automatic-Chord-Recogniton (ACR), key-detection or Cover-Song-Identification (CSI). We use here for CSI the deep-chroma of [MB17] named crema-PCP.